熱雑音とは
半導体を含め電子部品すべての抵抗体からは、周囲温度が絶対零度でない限り、常に内部自由電子の不規則な熱振動によって生じる熱雑音(サーマルノイズ)と呼ばれる雑音が発生します。
低ノイズプリアンプや微小信号センサなどを設計する際、入力回路部品の熱雑音よりも小さい入力換算雑音を実現することは不可能です。
よって、入力換算雑音を低くするためには熱雑音をいかに低くするかが鍵となります。
本記事の冒頭で熱雑音の計算フォーマットを記載しましたが、熱雑音の電圧Vn[Vrms]は下式で表されます。
$${Vn}=\sqrt{4kTRΔf}$$
k:ボルツマン定数[J/K](1.38×10-23)
T:絶対温度[K](℃+273.16)
R:抵抗値[Ω]
Δf:帯域幅[Hz]
上記の帯域幅に関して、熱雑音を発する抵抗以降の回路の周波数特性が、下図のようにある周波数まで一定でそれ以降急峻に低下するという特性を有するものであれば、その周波数までの帯域幅で計算すればいいのですが、実際はこのような理想的な周波数特性を有しているわけでないので、回路全体のノイズ計算は非常に複雑になります。
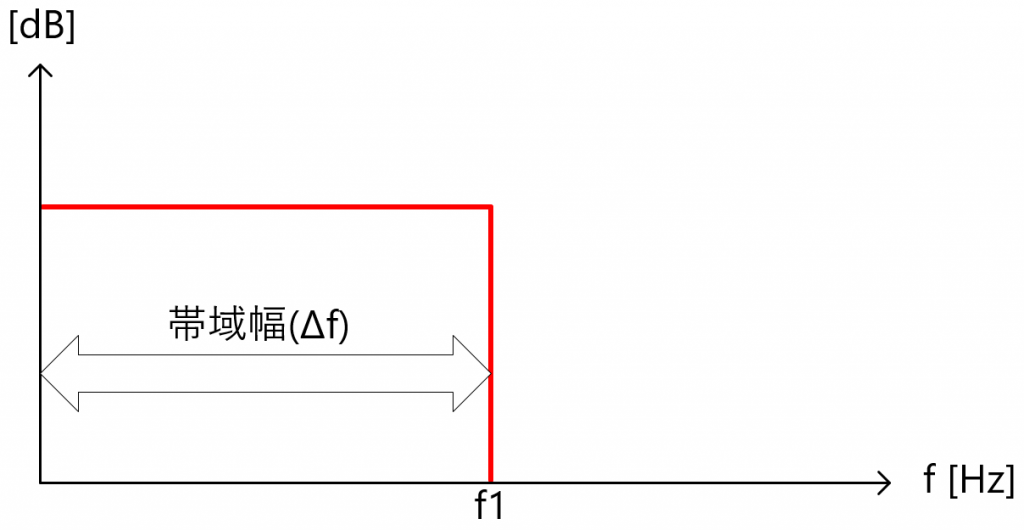
ただし、熱雑音の振幅分布はガウス分布であるため、平坦な周波数スペクトルとなる白色雑音(ホワイト・ノイズ)であり、等価雑音帯域幅の考え方を用いれば計算は簡単になります。(上式のΔf:帯域幅[Hz]を等価雑音帯域幅[Hz]として計算する)
等価雑音帯域幅
等価雑音帯域幅fNは、白色雑音の実効値を計算するときに用いるものです。ここで、周波数特性として回路が1つの極(1次)を持つ場合を考えると、以下の式で計算できます。
$${f_N}=\int_0^\infty \frac{df}{1+(\frac{f}{f_c})^2} = \frac{π}{2}f_c = 1.57f_c$$
fc:-3dBカットオフ周波数帯域
上式は単一極(1次)回路の等価雑音帯域幅であり、カットオフ周波数(fc)-3dB帯域幅の1.57倍大きくなります。下図に周波数特性を示します。
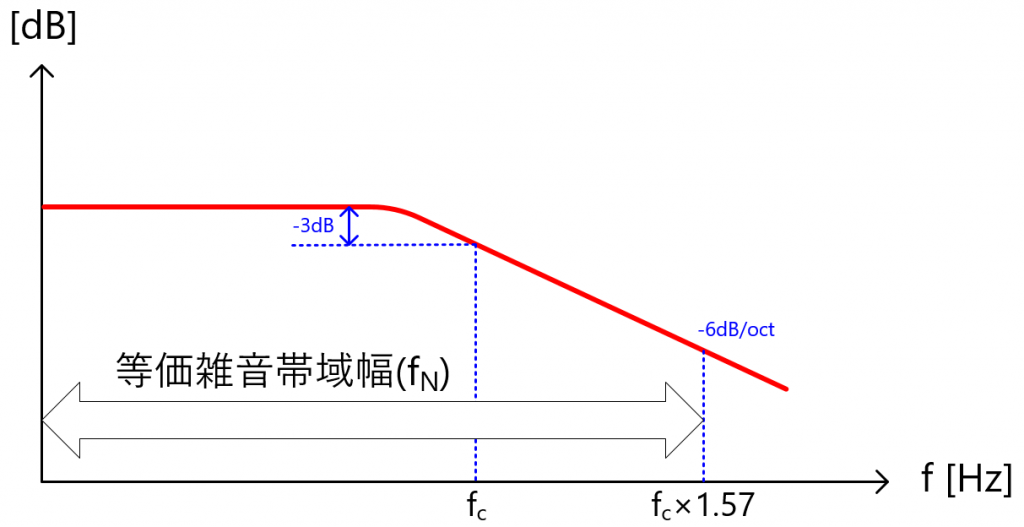
回路の極(次数)が変わった場合の等価雑音帯域幅を下表に示します。
| 極(次数) | 減衰傾度 | 等価雑音帯域幅 |
| 1 | -6dB/oct | 1.57×fc |
| 2 | -12dB/oct | 1.11×fc |
| 3 | -18dB/oct | 1.05×fc |
| 4 | -24dB/oct | 1.03×fc |
減衰傾度とは、周波数特性の傾きを表現したもので、単位はdB/octです。
1オクターブ上がると周波数は2倍になるので、周波数が倍になったときにどれだけ減衰しているかをデシベルで表したものです。
抵抗の熱雑音は、この等価雑音帯域幅を、前述した熱雑音計算の帯域幅Δfに代入し算出します。
熱雑音の影響
それでは、一般的なアンプの入力回路において、どうすれば抵抗の熱雑音の影響を小さくできるのか記載します。
おなじみの増幅回路において、熱雑音の影響が大きい箇所を下図の赤点線枠で示します。
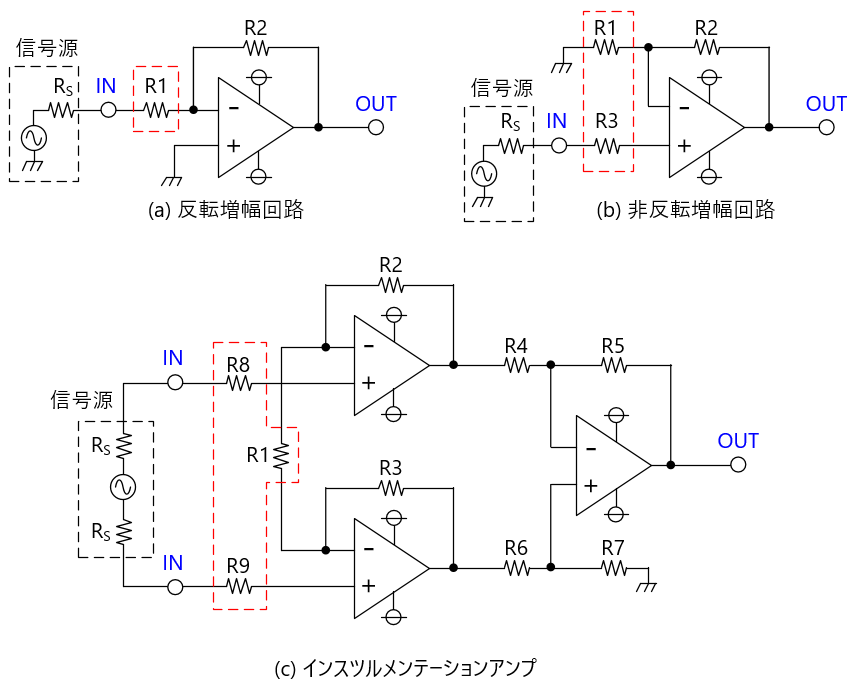
(a)反転増幅回路
入力に直列に挿入された抵抗R1の熱雑音の影響が支配的となります。
反転増幅回路は、R1とR2によりゲインが決まりますが、入力インピーダンスはR1にほぼ等しくなります。
熱雑音の影響を小さくするためにはR1を小さくしたいところですが、R1を小さくすると入力インピーダンスが下がり、入力信号は信号源抵抗RSとR1の分圧により小さくなってしまい、本来の回路仕様に影響が出てしまいます。
よって、反転増幅回路は低ノイズアンプに適していません。
(b)非反転増幅回路
入力に直列に挿入された保護抵抗R3とゲインを決定するR1の熱雑音の影響が支配的となります。
非反転増幅回路の入力インピーダンスは非常に大きな値であり、保護抵抗R3は極力小さくできます。また、ゲインを決めるR1は直接入力インピーダンスに影響しないため、熱雑音の発生が少ない小さな値にすることができます。
よって、非反転増幅回路は低ノイズアンプに適しています。
(c)インスツルメンテーションアンプ
入力に直列に挿入された保護抵抗R8,R9とゲインを決定するR1の熱雑音の影響が支配的となります。
インスツルメンテーションアンプは差動入力ですが、非反転増幅回路と同様に入力インピーダンスは非常に大きな値であり、保護抵抗R8,R9は極力小さくできます。また、ゲインを決めるR1は直接入力インピーダンスに影響しないため、熱雑音の発生が少ない小さな値にすることができます。
電子部品から発生する雑音には、ショット雑音やフリッカ雑音など様々なものがありますが、抵抗体から発生する熱雑音は非常に重要であり、注意すべきものだと私は思っています。
低ノイズオーディオ回路や微小信号センサ回路など、極力ノイズの影響を排除したい場合は、しっかりと検討し設計すべきです。
私が担当する設計は必ずオーディオ回路がありますので、この記事冒頭にある熱雑音の計算を頻繁に行っております。
