プリエンファシスとディエンファシス

プリエンファシスとディエンファシス

プリエンファシス(Pre-Emphasis)とは、かつてレコードやCDへのオーディオデータ記録において用いられた手法であり、オーディオ信号の中で相対的にレベルが小さくなる高域成分を増幅させ、S/Nを改善させる処理です。
ディエンファシス(De-Emphasis)とは、プリエンファシスによって高域が増幅されたオーディオ信号を、プリエンファシスとは逆の処理を行い、周波数特性を元に戻す処理です。

この工夫は、ADコンバータ/DAコンバータを有するオーディオ回路システムでも活用できます。
アナログ信号をデジタル信号に変換するADコンバータ手前でプリエンファシスすることにより、信号レベルが小さくなる高域成分が増幅され、高域成分のS/N比が改善し、デジタル化した信号の全周波数における品質が向上します。
※S/N比とは、信号とノイズの比であり、S/N比が悪いと信号とノイズのレベル差が小さいため、デジタル的に信号を増幅するとノイズも同様に増幅され、ノイズが目立ってしまいます。

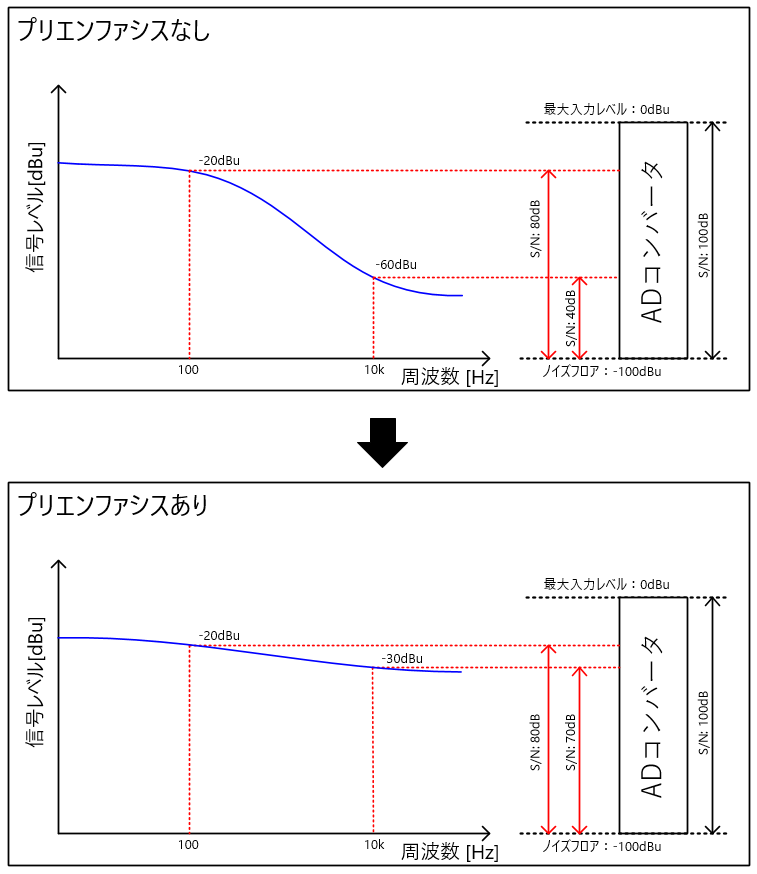
プリエンファシスの効果を下図に示します。
極端な例ですが、「プリエンファシスなし」の場合、信号の高域レベルが小さくなるため、ADコンバータでアナログ信号をデジタル変換した際、100Hzと10kHzの信号対ADコンバータノイズのS/N比は40dBもあります。
一方、「プリエンファシスあり」の場合、信号の高域レベルを増幅するため、デジタル変換した100Hzと10kHzのS/N比は10dBに縮まります。

CDのプリエンファシス

プリエンファシス特性は、規格で定められており、以下の式となります。
$${プリエンファシス特性}=\sqrt{1+(\frac{ω}{ω_x})^2}$$
$${ここで、ω=2πf}$$
CDのプリエンファシス特性における時定数は、以下で規定されています。
$${50μS}/{15μS}$$
$${ここで、τ_0=50μS=\frac{1}{ω_0},τ_1=15μS=\frac{1}{ω_1}}$$
よって、周波数特性で表すと以下となります。
$${周波数特性利得}=\frac{\sqrt{1+(\frac{ω}{ω_0})^2}}{\sqrt{1+(\frac{ω}{ω_1})^2}}=\frac{\sqrt{1+(2πfτ_0)^2}}{\sqrt{1+(2πfτ_1)^2}}$$
また、dBで算出すると以下となる。
$${周波数特性[dB]}=20{LOG}\frac{\sqrt{1+(2πfτ_0)^2}}{\sqrt{1+(2πfτ_1)^2}}$$
この特性を以下のグラフで表します。

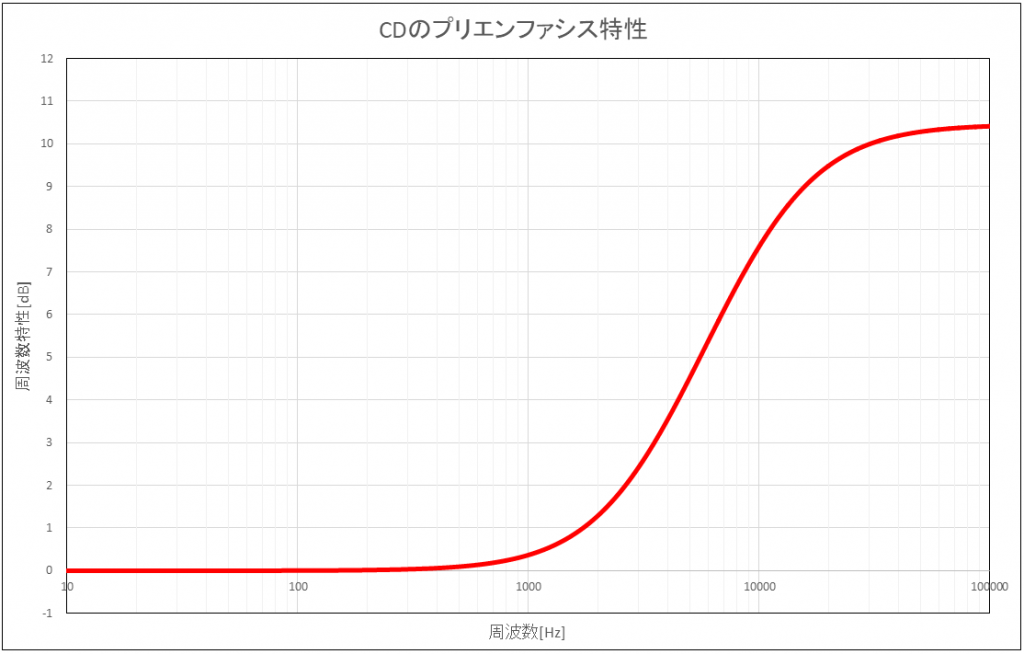
CDのプリエンファシス特性は、0Hzに対して、3.5kHzで3dB利得、6.9kHzで6dB利得があり、10.4dB利得で収束します。
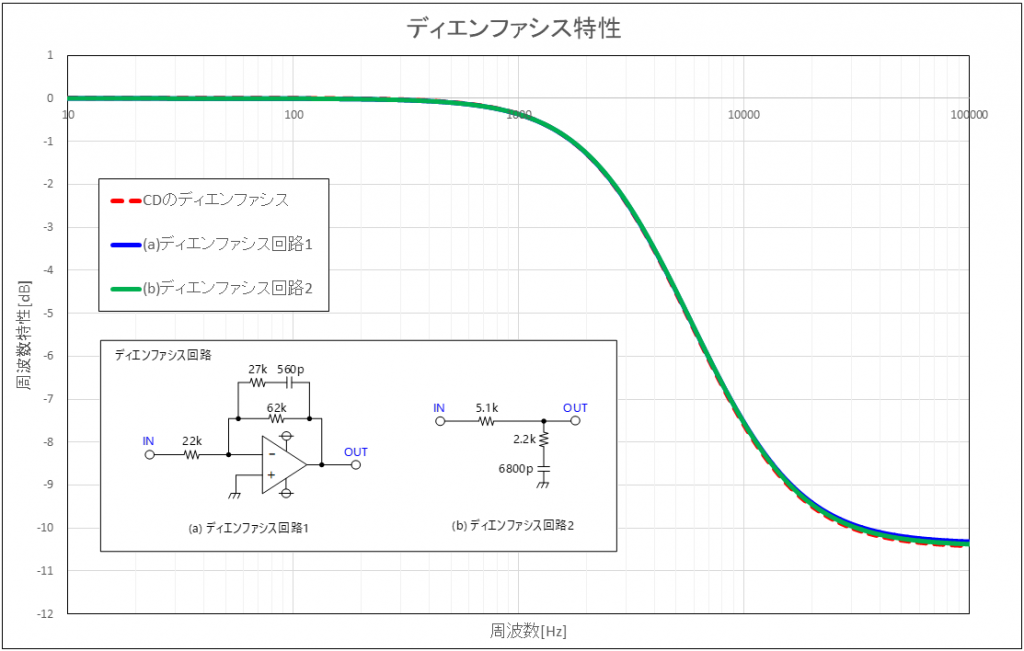
CDのディエンファシス特性は、プリエンファシスと逆の特性となります。

プリエンファシス回路とディエンファシス回路

ここで、プリエンファシスとディエンファシスを実現する回路を以下に示します。
オペアンプを使用した場合と抵抗・コンデンサのみ使用の場合を示しています。
下図では反転増幅回路を例としていますが、回路の都合により非反転増幅回路でも可能です。

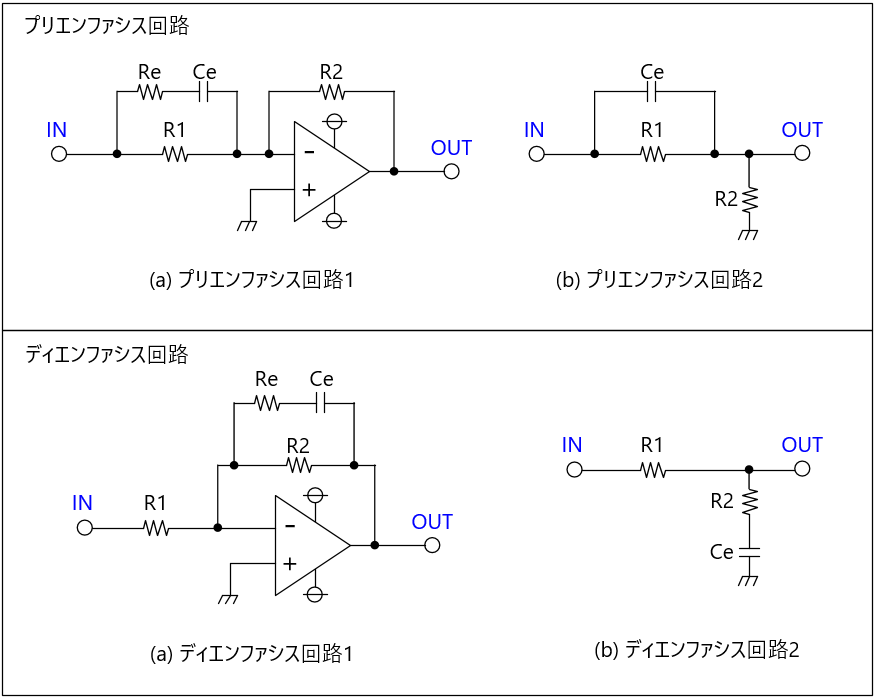
抵抗・コンデンサのみの回路は信号の減衰しかできませんが、オペアンプを使用すると信号の増幅ができるため、プリエンファシスではオペアンプを使用した方が好都合の場面が多いです。
また、抵抗・コンデンサのみの場合は、前後回路のインピーダンスによって周波数特性に影響があるため注意が必要です。

回路の動作としては単純です。
(a)のオペアンプを用いた回路は、コンデンサ(Ce)のインピーダンスが周波数特性を有するので、周波数によって抵抗ReとR1又はReとR2を含むインピーダンスが変化し、回路のゲインが変わります。

(b)の抵抗・コンデンサのみの回路も、コンデンサ(Ce)のインピーダンスが周波数特性を有するので、周波数によって抵抗R1又はR2を含むインピーダンスが変化し、抵抗分圧での減衰量が変わります。

R1とR2の値により周波数0Hzでの回路の増幅量又は減衰量が決まり、抵抗ReとコンデンサCeを調整することで周波数特性が決まります。
周波数特性の計算において、コンデンサのインピーダンスZcは以下の通り複素数で表現するため、抵抗とのインピーダンス計算では、複素数で計算した後、絶対値を取ります。
$${Z_c=\frac{1}{jωC_e}}$$
複素数の計算は、以下に示すExcelの関数を使うと簡単です。
・COMPLEX関数：２つの数値を虚数単位で結びつけて複素数に変換
・IMABS関数：複素数の絶対値を計算
・IMSUM関数：複素数の和を計算
・IMSUB関数：複素数の差を計算
・IMPRODUCT関数：複素数の積を計算
・IMDIV関数：複素数の商を計算

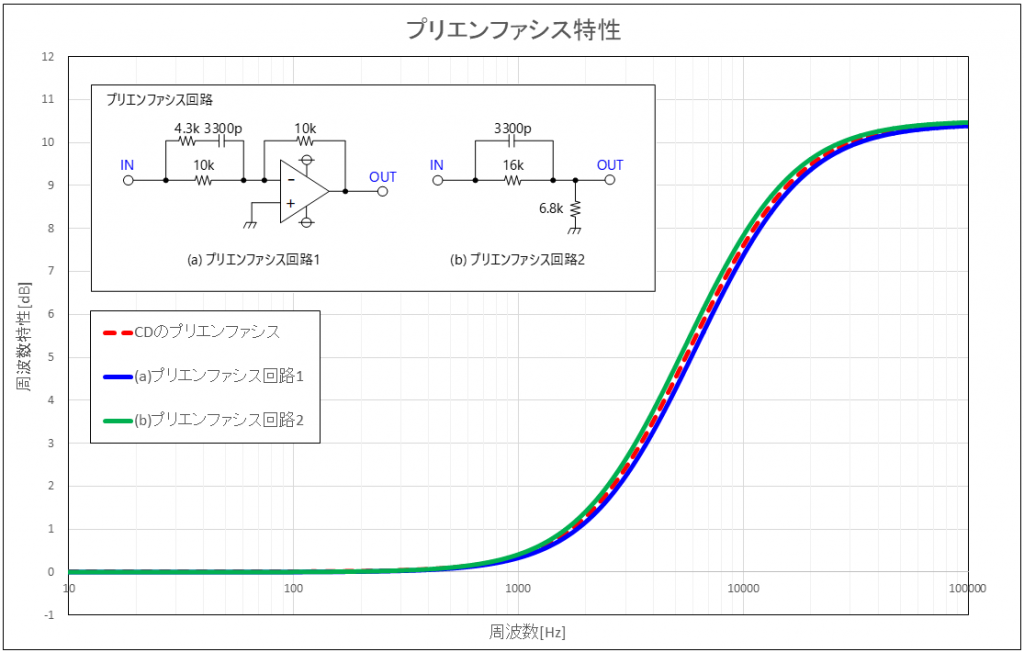
最後に、上図で示した回路が、CDのプリエンファシスとディエンファシスと近い特性になる値を決めて、その特性をグラフに示します。
尚、抵抗・コンデンサはE24系列から選定しており、ざっくり決めています。
また、各周波数特性は、0Hzの増幅量又は減衰量からの相対値としてグラフで示しています。